Vibration Damping with Shunted Reluctance Force Dampers
| Led by: | Dr.-Ing. Sebastian Tatzko |
| E-Mail: | jahn@ids.uni-hannover.de |
| Team: | Martin Jahn |
| Year: | 2023 |
| Duration: | 2023-31.08.2025 |
Project describtion






The reluctance force is the force that causes the attraction of two objects within the same magnetic field. To prevent so-called sticking, the reluctance force is mostly used in actively controlled systems for vibration damping. Passively operating shunted reluctance force dampers have been investigated comparatively little to date. In a preliminary study preceding the project, it was shown that the damping effect of a reluctance force damper is significantly enhanced by electrical resonance - similar to vibration absorbtion - in a narrow frequency band. One of the aims of the project is to investigate whether it is possible to increase the damping effect at several frequencies.
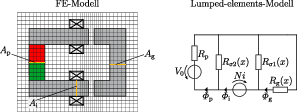
In addition to the desired magnetic flux, there are always parasitic leakage fluxes in a reluctance force damper and its surroundings, which cannot be described with sufficient accuracy by simple numerical models. To improve the calculation accuracy, the relationship between air gap length, electric field excitation and actual magnetic flux is therefore to be determined with a finite element model, taking into account leakage fluxes. (Figure 1)
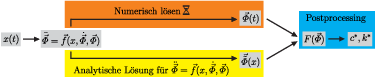
The dynamic behavior of a shunted reluctance force damper is described by non-linear physical relations, so that advanced numerical methods are required for calculation. On the one hand, these require computing time, on the other hand, the dependence of the system behavior on individual parameters is lost, so that parameter studies require a large number of numerical solution calculations. For the direct determination of parameter dependencies, an analytical approximate solution for parameters of the dynamic behavior is to be determined, containing the system parameters in explicit form. (Figure 2)
In the preliminary work preceding the project, it was observed that the frequency dependence of shunted reluctance force dampers is particularly advantageous compared to other dampers in vibration isolation applications. Here, calculations are to be carried out on a vibrating system, which is to be isolated by a shunted reluctance force damper from a vibration source. Moreover, the damping of force-excited systems is investigated. In addition to single-mass oscillators, oscillating beam structures are also considered. (Figure 3)


